住宅の屋根について (2022.07.25改訂版)

0．はじめに

　本稿では、住宅ストラクチャーの自作について、とりわけ屋根周辺に着目して考察を試みたいと思います。本題に入る前に、本稿のスタンスを三点明確化しておくこととします。

　第一に、私は専ら2Dcadや手書きで展開図を作成し、切り出して組み立てるといった方法を採っております。3Dcadを使用すれば本稿の手法よりもヨリ感覚的に、一気に造形できるのではないかとは常々思いつつ、ついつい展開図法に逃避しがちで、そろそろ3Dも勉強しなければ…というのが現状です。展開図が前提となる以上、3D設計が可能な方にとっては以下の内容はあまり参考になるものではないようにも思われます。予めご了承ください。

　第二に、本稿は住宅の屋根設計を中心にご紹介します。これは、私がストラクチャーの製作を始めた当初、特に屋根周りの設計がよくわからず、且つ調べてもあまり情報が得られなかったように感じるためです。屋根は、その形状如何では自作の際に障壁になりやすい場所ではないかと推察するに、私としてもどのような設計手法があるのかは興味深いところです。そこで、以前より別サイトにて本テーマについて記事にしてみようか…とは思いつつ、内容的にもあまり人に勧められるような手法ではないため、躊躇っておりました。このような不完全なものを人目に晒すべきではないというのは重々承知の上、本サイトはジオラマSNSということで、多少マニアックでアバウトな内容も許されるのでは…と思い、今回投稿してみる次第です。ジャンル分けにも悩みましたが、建物自体を取り上げるわけではないため、「街並み」ともいかず、さしあたり「テクニック」とさせていただきました。

　第三に、本稿における設計に当たっては数Ⅰ・Ⅱ程度の三角比を使用します。私自身文系学生であり、数Ⅲはほぼ未履修で立ち入ることができず、数学事項に関しても厳密な証明等はできかねます。また、建築模型とも無縁で、その分野固有の製作法についてもよくわからないというのが正直なところです。あくまでも、中途半端な知識のもと使用してきた手法にすぎないものですので、その点もお含みおきください。本稿の内容により何らかの不利益が生じても、執筆者としては一切の責任を負いかねます。本稿をアップするにあたり、一応自身で再現性のチェックは行いましたが、間違っている箇所があることも容易に想定されますので、もし誤りを発見された場合はコメント等で遠慮なくご指摘いただければと思います。よろしくお願いいたします。

　以上、前置きがくどくなりましたが、本編へ入っていきたいと思います。

1-1．寄棟屋根(標準)：設計準備

　住宅を設計する場合、まずは直方体＋切り妻屋根が一番シンプルなように思います。ただ、Google Earthなどで街並みを俯瞰するに、寄棟屋根(下図参照)もかなり多く、その再現もしたくなってくるものです。そこで、まずは長方形のベースの上に寄棟屋根を作成する方法を本稿における基本パターンとして概観できればと思います。
　
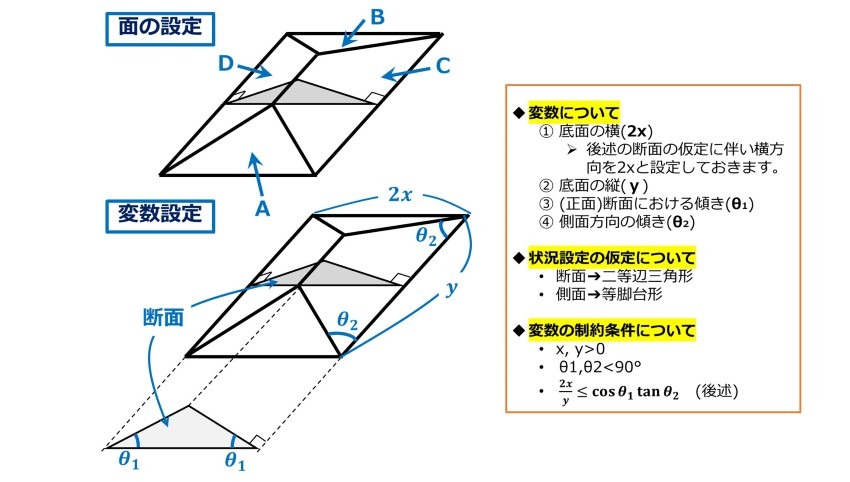
　まずは、寄棟屋根を構成する底面＋4面(A～D)を下の図のように設定します。

　続いて、図中の順番とは左右しますが、状況設定を行っておきます。今回の設定のポイントは次の二点です。
　第一に、正面から見た面(A面および断面)は二等辺三角形を仮定します。実例を見ても屋根は左右対称であることが多いほか、変数(θ)が増えすぎると一般化が困難になる点、対称形を増やしておくことで平行な辺、等角が増える点を考慮してのことです(これらの点は新規に図面を作成する際に有効です。詳しくは4章にて後述することとします)。
　第二に、C面は等脚台形を仮定しておきます。勿論C面の縛りを緩めて台形にとどめておくことは可能で、そうした実例もあると思われますが、先述の変数増加を回避する観点から今回は見送ります。

　設定状況を踏まえて変数をおきます。今回はx，y，θ1，θ2の4つです。変数の置き方についてはいろいろ考え得るところですが、鉛直方向は断面の角(θ1)を用いて表現してみました。θを用いておくことで使用可能な公式が増えるほか、鉛直方向を数値設定すると三平方の定理に依存し、累乗計算が増えて一般化が面倒にもなるので、できるだけθを用いるのが良いと思います。また、今回A面は二等辺三角形を仮定したことで、頂点より底辺におろした垂線の足は底辺の中点と一致するため、一辺を2xとして処理します。

　変数を設定したため、一応制約条件も併せて設定しておきます。経験上、単純な寄棟屋根の場合はいきなり作図に取り掛かっても支障はほぼなく、考慮に置かずとも問題ないとは思いますが、特に傾斜を緩めた場合には稀に作図不能になることがあるため、事前に仮定した状況にしたがって制約式を立てておくと安心です。尤も、以下に掲げた変数の制約条件のうち上二つは自明のため、3つ目のxとyの関係式をご確認いただければと思います。この式は諸々の仮定を基に立式したものであるため(導出は1-2にて後述)、状況設定を変更する際は制約式もそれらに依存する点を留意する必要があります。
　念のため、xとyの関係式が等号成立の場合、屋根の形は方形屋根のように三角形4つで構成される形状となります。

1-2．寄棟屋根(標準)：辺の長さのまとめ

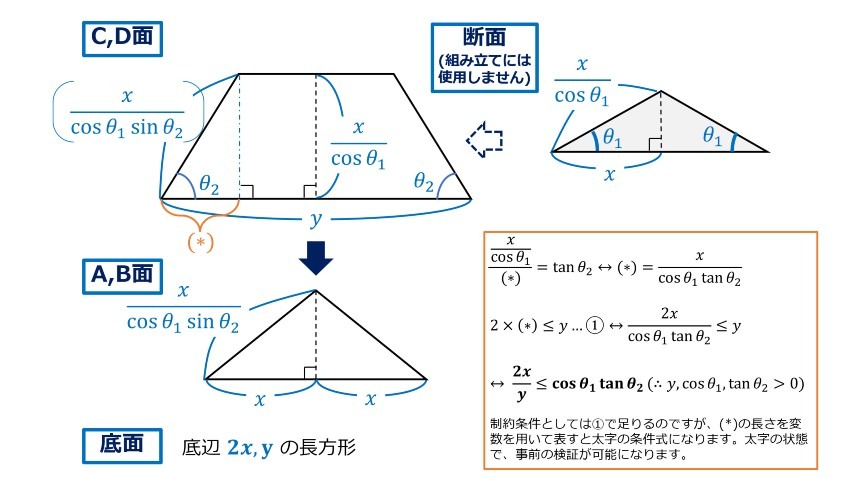
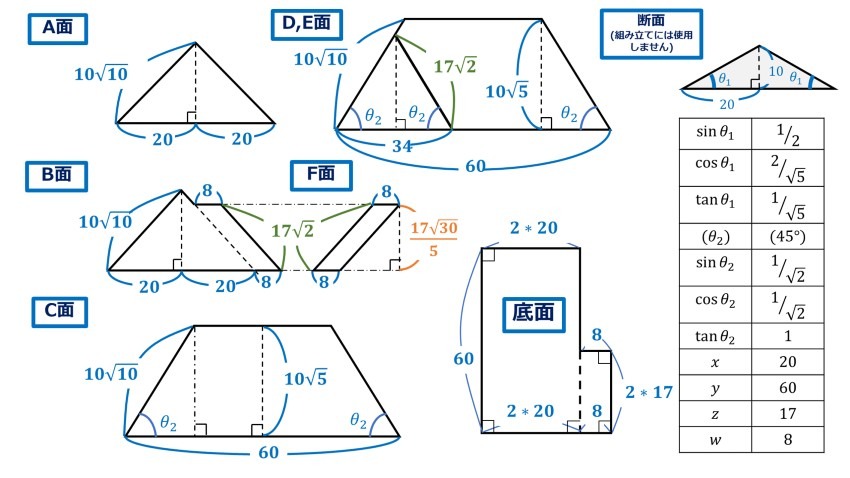
　仮定に基づき、変数を用いて各辺を表すと下図のようになります。図中の式に変数の値を代入すれば、展開図の作成が可能となります。

　ちなみに、先に述べたx,y間の条件制約については、下図中のオレンジの囲みをご参照ください。この式はC,D面を等脚台形(等号成立時は二等辺三角形)にするためのものです。すなわち、今回の設定の下では２×(＊)≦yを変数を用いて表したに過ぎません。繰り返しにはなりますが、C,D面の傾きを変更し、等脚台形の仮定を外した際は、上記関係式についても変更が必要です。

(※本稿に掲げる図については、すべて適当に作図しているものであり、正しい寸法ではありません。)

3-1．寄棟屋根(発展形)：序

　既に文字数がかさんできてしまっておりますが、ここからが本稿の本丸です。連続性のある内容なので、続けて書くこととします。
　
　ここで再度Google Earthで適当な住宅街を俯瞰していただくと、寄棟屋根ではあれど、一部が張り出しているなどして、かなり複雑な形状をしている住宅が意外にも多いことがご確認いただけるかと思います。本体に切り欠きを入れてベランダを設置するように、建物はその本体が直方体単体で完結しているものは少なく、寧ろ直方体を幾つか組み合わせたような複雑な形状をしており、それに従って屋根も構成されているといえるでしょう。最近の建売住宅などは特にこの傾向が強いように感じます。
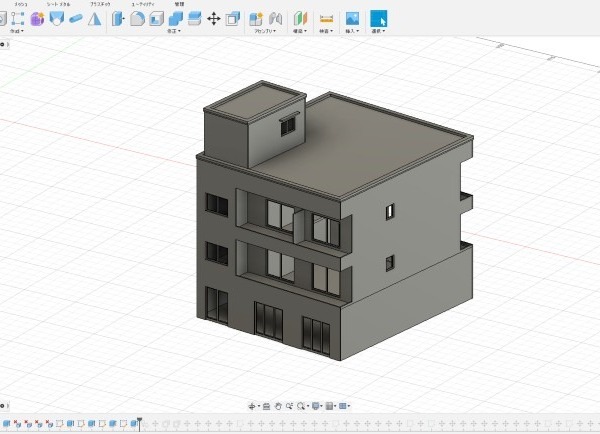
　そこで、屋根のベースを単なる長方形から一部が張り出した形状に変更の上、それに対応した屋根の製作方法の一例について述べることとします。実は、前回の投稿にてご紹介した住宅街ジオラマは、住宅の自作練習を目的としており、屋根の形状について上記の観点から意図的に変化を加えました。例えば、以下の写真中央付近の2棟はいずれも寄棟屋根に張り出しを設けた形状としています。そこで、本稿では、そのうち写真右側の屋根を例にまとめてみたいと思います。

3-2．寄棟屋根(発展形)：設計準備

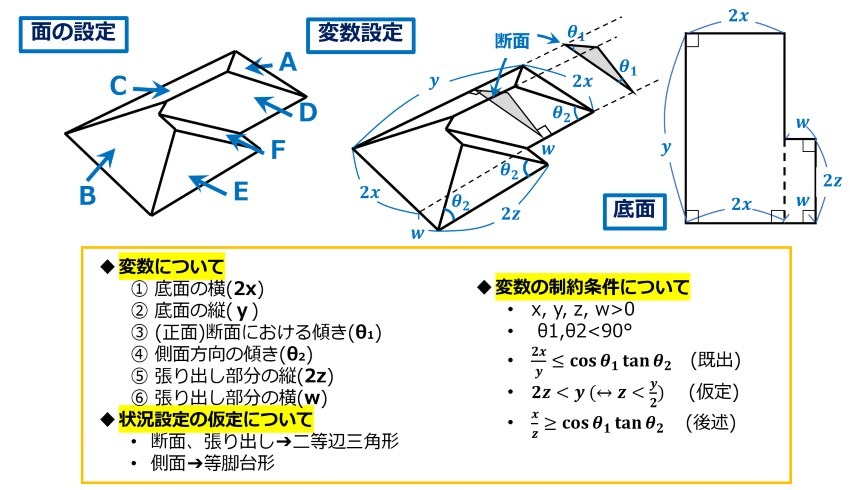
　まずは、寄棟屋根を構成する底面＋6面(A～D＋E,F)を下の図のように設定します。

　続いて、ここでも状況設定を行っておきます。A面、C面の仮定については2章と同じくそれぞれ二等辺三角形、等脚台形とします。変更点は、①屋根の底面を長方形+αと変更したのに伴い、E,F面が新たに登場する、②B面がA面とは異なった形となる、の2点です。ここで、E面についても二等辺三角形を仮定することとします。こうすることで裾の角についてθ２を使いまわすことができるほか、平行な関係からA面+F面＝B面が成り立つので処理が簡略になるなどメリットがあります(この点については4章にて後述します)。

　設定に従い、変数をおきます。今回はx，y，θ1，θ2，w，zの6つです。先述の通りE面を二等辺三角形としたため、θの増加はありません。E面については先の仮定により、二等辺三角形の頂点より底辺に下ろした垂線の足は底辺の中点と一致するため、一辺を2zとして処理します。

　変数を設定したため、ここでも制約条件も併せて設定しておきます。5つ掲げたうちの上3つは2章と同じ議論であり、4は図より明らかなため、割愛します。5つ目の条件はx,zの関係に係るものですが、こちらは意外とエラーになりやすいので、事前のチェックが効果的です。繰り返しにはなりますが、3、５番目の式は(3-1)の仮定を基に立式したものであるため(新出の5について導出は3-3にて後述)、状況設定を変更する際は制約式もその設定に依存する点を併せてご注意ください。念のため、5番目のxとzの関係式が等号成立の場合、B面が等脚台形となります。

3-3．寄棟屋根(発展形)：辺の長さのまとめ

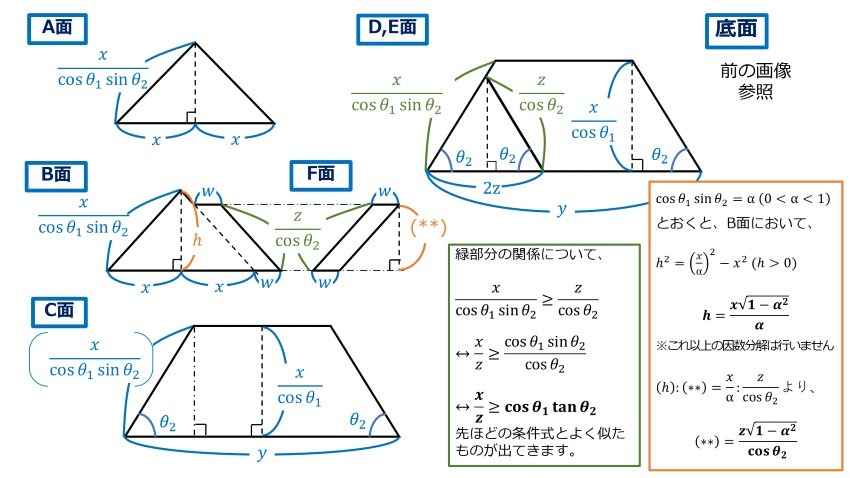
　仮定に基づき、変数を用いて各辺を表すと下図のようになります。図中の式に変数の値を代入すれば、展開図の作成が可能となります。

　先にご紹介したx,z間の条件制約の導出過程については、図中緑の囲みをご参照ください。この式はB面において、A面と合同な三角形の高さ(h)を、隣につけ足した平行四辺形(F面と対称形)の高さ(**)が上回らないようにするためです。後者の高さ(**)の算出に当たっては、前者の高さ(h)を基に比例配分をして算出しています(算出過程は図中オレンジの囲みを参照)。比例配分についての詳細は4章にて後述します。

3-4．数値代入例について

　これまでの図表は見た目の複雑さが印象に残りがちなように思い、数値代入例を掲載してみます。下図の数値は実際に組み立ててチェックを行ったものになります。
　今回は図中の表にまとめた通りに設定しました。θについては、sin、cos、tanのどれかがわかればほかの二つは関係公式から導けるため、代入計算前に3つすべてを明らかにしておくと後々代入しやすくなります。代入の際は分母に三角比が入ることが多いので、逆数の処理のミスさえしなければ計算自体はそう複雑ではありません。

　作図に関して三点補足をさせていただきます。
　第一に、これまでに示した辺の長さは過剰拘束気味に表記しているため、すべてを求めなければ作図ができないということはありません。今回は設定の段階で意図的に平行が多く生じるようにしているため、平行四辺形の対辺の長さが等しいなどの図形的性質を応用すれば、作図の場合はコンパスで、2Dcadの場合は機能を利用して具体的数値はわからずとも長さを図り取ることが可能です。こうした手法を合わせて活用すれば、より早く作図が可能かと思います。
　第二に、過剰拘束気味に各辺の長さを設定している都合で、2Dcadで作図し、且つ辺の長さを上位で四捨五入した場合は、一致すべき点がずれてくるなどの弊害が生じます。私が使用しているJw_cadは指数での数値設定が可能ですので、可能であればルートについては概数でなく1/2乗で入力するのが安全です。一方、手書きで作図する場合については、小数点以下の管理が難しいこともあってこうした問題自体をあまり気にすることは多くなく、三角比を持ち出した意義は薄れますが、コンパス頼みでも十分に仕上がると思います。
　第三に、これまでに示した手法により算出された寸法は、素材の厚みを考慮に入れておらず、単に理論値に過ぎません。もっとも、屋根のように斜めに部材を組み合わせる際は、パーツの角を斜めに落としておけば事足りるので、図面上で微調整は行わずとも対応が可能と考えています。そのため、本稿では素材の厚みについて設計段階での調整は捨象し、組み立て時の微調整に委ねることとしています。

3-5．さらなる展開

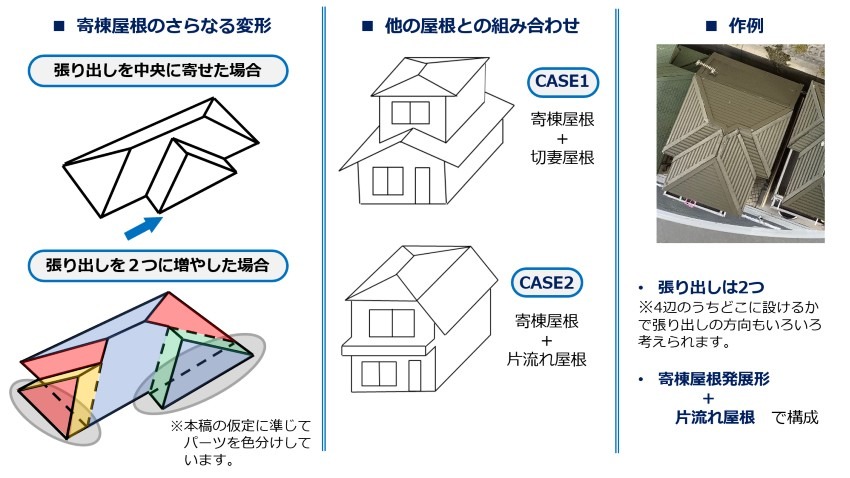
　以上、寄棟屋根＋αの作例についてご紹介してきました。しかし、作例以外にも、多様な「+α」の方法が考えられます。例えば、張り出しひとつとっても、①場所を変える、②数を変えるといった変更が可能です。以下の図においては、①について張り出しを中央付近に設けた形状、②については張り出しを2か所設けた形状を掲載してみました。どちらもありそうな印象です。
　他の拡張例として、ほかの屋根とのコンビネーションも有効です。下図においては①切り妻屋根と組み合わせた例、②片流れ屋根と組み合わせた例を取り上げてみました。このように、形状間の組み合わせによりバリエーションが確保できると思います。

　こうした拡張の作例として、手前味噌ではありますが、再び住宅ジオラマのうち1棟をご紹介します。中央付近の住宅は、寄棟屋根＋張り出し2つ＋片流れ屋根のコンビネーションを取り入れたものです。

4．新規作成時の考え方

　2章・3章は屋根を展開図化できることを前提に、三角比を用いてその辺の長さを表すことに焦点を当ててきました。しかし、そもそも展開図化の際に混乱が生じることも多々あります。混乱を避けるにあたって、私は次の2点を考慮しています。
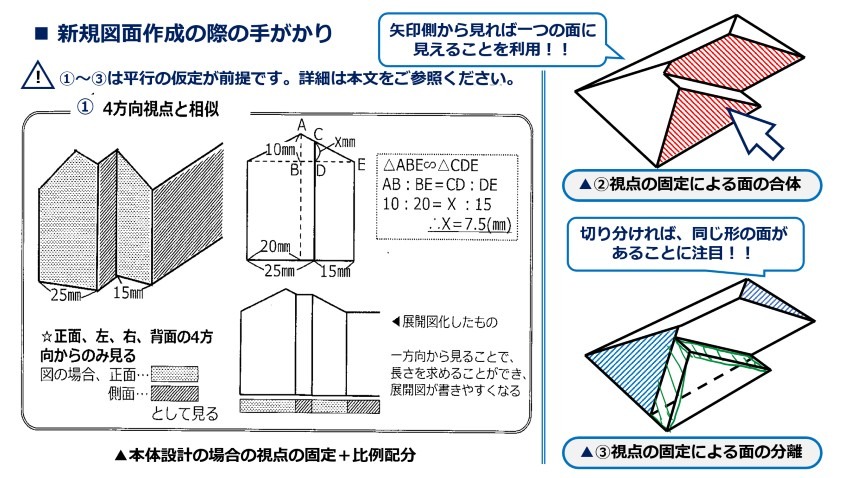
　第一に、展開図化の際に、視点を正面、左、右、背面の4面に固定する(すなわち斜めから見ない)ことです。特定の方向から見ることで、形が複雑な面についても、下図中②のように実はまとまった形の面を切り分けた結果生じていること、下図中③のように切り分ければ単純な形の面に戻ることが明らかになったりします。

　しかし、このような見方をするためには条件があります。例えば下図②の場合であれば、赤く斜線を入れた面が平行でなければ面をスライドして1つの面に組み合わせるということがそもそも不可能です。すなわち、4方向視点を可能にするには、平行な辺、等角を増やしておく必要があるのです。2章・3章の設定の段階で角を揃え平行な辺や面を多くしていたのはこのような事情によります。
　そこで、第二の考慮要素として、設計の際に平行な辺や角を増やしておくことが重要になってきます。平行な辺や角の増加は4方向視点を可能にするのみならず、寸法把握の場面でも有利に働きます。平行線における同位角や錯角の関係を通じて等角が増えれば、相似な図形が増えるからです。相似な図形が増えれば、相似な図形同士は辺の比が等しいことを利用し、未知の辺に対しても比例配分での算出が可能になります。詳しくは下図の①の計算例をご参照ください。

　以上の2点を活用すると、屋根を平面の展開図に落とし込むことが比較的容易になるのではないかと考えています。

5．おわりに

　最後まで目を通していただき、本当にありがとうございます。ダラダラと読みにくいばかりか、内容としてもジオラマ投稿ともつかぬ怪文書になってしまいました。お目汚し失礼いたしました。製作過程について一丁前に語れるような身でもないので、なかなか公開は緊張するものですが、本稿の内容はかねてより何度かまとめようとしたものの振り切れずに下書き状態にあったため、今回ひとまず形にすることができて投稿者としては満足です。
　最後に、本稿の手法は最適解でも何でもなく、不正確な点、もっと効率化できる点、別の方法が存在するものと思います。お気づきの点等ございましたらコメント等でご連絡いただけますと幸いです。

補記(2022.07.25)
　屋根以外の住宅ストラクチャー製作工程については、以下のリンクにてまとめています。こちらも自己流ではありますが、よろしければご覧ください。
https://note.com/cheerful_ruins2/n/nb924c9f1552c